Emotional Intelligence in Mathematics Education

Introduction

I am a student, pursuing pedagogy in a renowned institution. I have a great potential in teaching learners mathematics, and as such, I have purposed to build my capacity, to be able to embrace a lasting improvement towards the subject. The experiences of my career pattern has been able to influence on my desire, as well as readiness to engage in continuous improvement activities and I believe that the emotional intelligence that I possess is able to influence the self-confidence and motivation to my learners. Another factor that has influenced my learning is the fact that I possess detailed and deep knowledge on mathematics, as well as the general pedagogical content, and as such, I am able to incorporate sufficient knowledge on learners’ strengths, weaknesses, cultural experiences, as well as learning styles. Skills are also important factors, which have impacted on my repertoire of significant teaching strategies that entails working through a vital learning cycle of reflection and evaluation, extraction of meaning, and also planning on using learning in the future. Overall, it is evident that motivation poses as a starting and ending point for learning mathematics. This can assist me in devoting my effort towards embracing change, as well as new learning. Through motivation, I am certain that I will make a good mathematics teacher to my learners, who will be able to make sense to them, as well as meaning in the mathematics lessons that I will have. In the future, when I will be done with my studies, and on practice, I want to be a good teacher, whose learners will easily understand various learning concepts on mathematics. Triangulation refers to a process in which data is looked at from a different perspective. In other words, it is a powerful technique that aids in the facilitation of data through significant cross-verification, based on two or more sources. Methodological triangulation uses different research techniques in addressing the same question (Herbal-Eisenmann & Breyfogle, 2005). For instance, a teacher can be interviewed regarding his or her teaching, and as such, the collected data is then compared to others that are obtained from other interviewees, observation of his/her teaching, examination of various comments that the teacher makes on the work of the students amongst other examples. The overall assumption is that an information can have biases, and as such, sound conclusions and even evidence can only be obtained from several sources of data. It is then worth noting that triangulation is used with the primary purpose of enhancing validity, in order to raise trustworthiness of vital interpretations (David, 2007). The primary purpose of this paper is the stress on the significance of questioning in the progress of student learning. In this regard, it will majorly use Bloom’s taxonomy, as well as Wragg and Brown (1993) ideology (Questioning in the Secondary school) in determining how this concept has improved and helped in the progress of student’s learning and the learning of a teacher. The list of questions that will be emphasized on, in this paper will be lesson 1: Solving Quadratics, Lesson 2: Completing the square, Lesson 3: Completing the square, Lesson 4: Completing the square graphically, Lesson 5- solving quadratics: mixed worded problems, Lesson 6: area of compound shapes, and Lesson 7: (i) Angles of Polygons (ii) Recurring decimals.

Literature Review

Questions/questioning is an important part of teaching. It is one of the basic ways by which the teacher helps in encouraging the student’s learning and thinking. According to Aschner (1961), he called the teacher “a professional question maker.” Certainly, teachers ask many questions during any given school day. It is evident that the major part of teaching time comprise of questioning, be it during preparation of a lesson or delivering lessons and talking to pupils (Wragg & Brown, 2001). Effective questioning includes establishing an appropriate environment, creating a climate conducive for learning, using a mixture of questions, practicing questions accurately, giving sufficient waiting time for response and using probes in response, to the answers provided by students. It is significant to take note of the fact that teachers need to consistently enhance various questioning skills through workshops, peer observations, and critique among others. In Mathematics, questioning poses as a common case. Questioning or testing in mathematics usually involves different numbers using the same knowledge. Some significant key facts have been followed, in mathematics, in order to be able to solve any problems for instance. (x +1)2 can be tested if they can use (2x+4)2. However again, they have foundation and higher sets. On the foundation stage, pupils are not taught or expected to learn (2x+4)2. This is because they do not get these kind of questions in examinations, and as such, it is like they are only prepared for passing for passing or getting good grades in examinations. This then leads to the question on why significant application fits (Wragg & Brown, 2001). Would it not be asking or learning similar questions to the ones, which students attempt in their classrooms? As such, a question also arises on whether HOT (analysis and evaluation) can be applied, especially at the foundation stage.

Questioning using Bloom’s taxonomy

Teachers often ask questions to their learners, yet it should be noted that not all questions appear on the same level. It is evident that some questions are usually easy to answer, whereas others often entail a great deal of thinking. In this regard, Bloom brought forth a taxonomy, to aid in composing questions, based on different levels of thinking. Of significant to note is the fact that Bloom’s taxonomy has heavily influenced teaching and assessments for over 50 years throughout the world. It can help working from low order thinking to high order thinking (Brown & Wragg, 2003). LOT includes knowledge and comprehension, whereas HOT includes skills of analysis and evaluation, It should be noted that application can be included in both categories because “new situations’ are required for applying the knowledge. It cannot be a “new situation or problem” if it is exactly like the one being done in the class with minor changes. It is also worth noting that the taxonomy ranges from low to high cognitive thinking levels. The levels include to create, evaluate, analyse, apply, understand and remember. On the ‘create’ level, which is the first going downwards, it involves putting elements together in a way, through generating, planning, and producing. The ‘evaluate’ level involves making judgements, based on standards through checking and critiquing (Arends & Castle, 1991). The ‘analyse’ level involves differentiating, organizing and having the ability to distinguish between components or parts. On the fourth level, which is ‘apply’ the learner implements knowledge to situations. On the fifth level, which is ‘understand,’ the learner can be able to construct meaning from different functions and use it is explaining various concepts. The last level, ‘remember,’ involves recalling previous knowledge.

This is as presented in the table below:

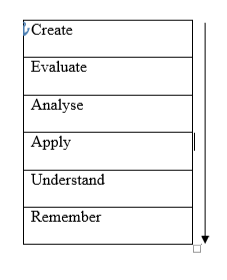
The differences between HOT and LOT are as provided as follows: Firstly, Lot follows rules whereas HOT discovers significant patterns. Secondly, LOT involves performing computation whereas HOT involves solving word problems. Thirdly, Lot entails vocabulary or definitions whereas HOT entails interpretation of information. Fourthly, LOT has simple applications, whereas HOT has complex applications. Fifthly, LOT entails procedural knowledge, whereas LOT entails conceptual knowledge (Bourner, 2003). Sixthly, LOT rates learning/ copying teacher whereas HOT entails analysing and critical thinking. This is as shown in the table below:

However, it is significant to take note of the fact that for exceeding results, a mixture of HOT and LOT questioning is required. For instance, in Mathematics, following rules is just as important as discovering patterns e.g the use of BODMAS rules is important, the rules of angles etc. However, it should as well be noted that learning why to use them is equally important but does the curriculum gives the teachers enough time needed to teach that? “SOW” needs to be followed. Majority of teachers teach “HOW” rather than focusing on “WHY,” which includes “mastery” and it is not very much appreciated and promoted yet, especially if students are going to sit in foundation test and are non-selective setting. However, it is successful in creating interest in the subject in order to motivate pupils to investigate or just follow the given rules (Koo, 1999).

Levels of knowledge

Factual- Students must know the basic elements to active problems. For instance, the key terms, and key facts

Conceptual- Interrelationship between the basic elements within a larger structure that enables the elements to function together. For example, principles, theories, and disciplinary areas.

Procedural- This is how to do somethings. It entails the methods of enquiry by use of skills, techniques, as well as methods.

Metacognitive- This is the awareness and knowledge of one’s own cognition. It is strategic or reflective knowledge about how to go about solving problems (Patel, 2003).

Methodology

Research design

Mathematics has been identified as a vital issue, which has an important impact on the preparation of the teacher. Although, it is evident that there have been extensive research. Conducted to determine the anxiety of mathematics, it is evident that more research have as well be identified to address issues, which would add towards the repertoire of available strategies for teachers and in enhancing the motivation of learners to learn mathematics. Literature reviews purpose to underpin the mathematics concepts (Mankiewicz, 2000). Taking into consideration, the ways in which teachers and learners can overcome mathematics anxiety, it is worth noting that the subject of this paper purposes to provide a research-based framework, which could aid in developing and describing the significant process in which mathematics teachers and learners can develop a positive identity. In turn, the theoretical model would aid in informing the repertoire of significant strategies, aiding in teacher preparation, and thus, contributing substantially to learners and education programs, not necessarily mathematics alone (Shahrill, 2013).

Grounded theory

Owing to the aforementioned facts, grounded theory, introduced by Glaser & Strauss (1967) is the most essential methodology, used in developing the aforementioned theory, in which data is grounded systematically, gathered, and also analysed. It is significant to take note of the fact that it is a research method, which allows for significant theory to be generated via comparison of other data sources. Notably, it pre-supposes that the concern may be illuminated using the accounts of people, based within an area of inquiry. It enables a theoretical model of the significant process that needs to be developed, as well as the patterns that are extracted from significant empirical data observations. It is also worth taking note of the fact that grounded theory requires that the method id repeated, there should be sampling, should entail a common themes, as well as coding of the participants’ experiences, until a point where there are no further concepts, which emerge. There are also differences in the approaches adopted in the grounded theory (Glaser & Strauss, 1967). However, it is evident that the Straussian approach poses as to be more useful for various studies of individuals. In this regard, it is noteworthy that this paper purposes to revisit the analysis conducted in previous research, by use of grounded theory perspective, and as such, it proposes it stresses that the next stage that should be undertaken should focus on the development of a significant theoretical framework. This is owing to the fact that it provides a significant background to the research and this includes the processes involved in grounded theory, which leads to the building of the framework, as well as a perspective on the progresses of data so far. Finally, the paper also purposes to provide a provisional framework, which would aid in underpinning the subsequent phase of the entire research (Glaser & Strauss, 1967). Overall, it is significant to take note of the fact that grounded theory was regarded as most essential for this study, owing to the fact that it purposes to understand the required action in a substantive area, based on the participant’s point of view, and also examines the participants’ behaviour that revolves around their area of concern, thus giving texture, as well as significant to their personal reflection. This paper is within the debates, and also the agendas of mathematics for teachers and learners and as such, it has long-term implications.

Content analysis

Mathematics is a subject, which entails frequent use of calculation, as well as functions written using numbers, theories, as well as proofs. In this regard, it is worth noting that it requires patience, as well as perseverance in logical, and critical thinking. Reasoning and understanding pose as critical factors that teachers should consider to enable their learners to learn mathematics easily (Holliday, 2002). Based on this paper, it is also notable that qualitative research would involve the use of content analysis. In contrast to other forms of qualitative research methods, it should be noted that content analysis is not in any way linked to a particular science, and as such, it requires a few rules to be followed. In this regard, there is a reduction in the risks of confusing matters that concern philosophical concepts, as well as discussions. In other qualitative research methods, it is often evident that the researcher is obligated to adhere to a particular qualitative perspectives, and as such, the main purpose is to achieve a rigor, as well as credibility, which makes the results to be trustworthy. However, in content analysis, different credibility concepts can be chosen, based on the trustworthiness of the discussion (Holliday, 2002). Overall, content analysis is defined as a research technique used in making replicable, as well as valid inferences from texts or any other meaningful matter to the context. Notably, it is more than a process of counting, as its primary goal is to link the derived results to the context, or even to the environment, in which they have been produced. In other words, it is a research method that purposes to provide a systematics, and also an objective means of making inference from visual, verbal or written data, for describing, and quantifying specific phenomena. Content analysis entails condensation (which is a process in which texts are shortened whilst still preserving the core meaning), coding of the responses of the participants, category (which is formed by grouping together the codes, which are related to one another, based on their content and context), and a common them (which are seen are expressing a meaning) (Holliday, 2002). Overall, this study also chooses content analysis, owing to the fact that its objectives is to systematically transform larger texts into highly organized, and also concise summary of the study’s key results. The analysis of raw data, derived from verbatim transcribed interviews aid in forming categories or rather themes, which is in other words, a process of abstracting data at every step of the analysis, primarily from the manifest, as well as lateral content to the latent meaning. Overall, it should be noted that having changed my general questioning to HOT questioning aided me in improving results, and students’ learning, as well as my own progress. I was able to impact their knowledge in mathematics significantly and made them understand complex content, which poses as an important role in scientific inquiry, and meaningful learning. Based on this fact, it is evident that I was able to tap all the existing knowledge, which needed the understanding of HOT questioning.

Critical analysis and discussion

The process of critical analysis involves reading, selecting, presenting, interpreting, and drawing conclusion. In critical analysis, the researcher is supposed to examine the presented analytical process, in order to check the validity, and thus, ensure that it stands up to searching and recognizing limitations. Of importance of critical analysis is to analyse the presented data. It is significant to take note of the fact that analysing qualitative data generally from a research is often challenging. However, it involves an innovative process. The data that is required during the learn phase would lead to the development of insights, which would in turn provide significant clues that aid in enhancing potential interventions (Moyer & Milewicz, 2002). This then brings forth the need for thematic analysis, which can be used in making sense of the unrealistic materials that seem senseless. In this regard, it can be used in analysing qualitative information, and also systematically gaining knowledge, as well as empathy on a person, interaction, situation, group or culture. Overall, it should be noted that thematic analysis is applied in an instance when there is need for problem framing, and as such, it aids researcher in moving from a broader reading of data towards discovering significant patters for specific research questions (Braun & Clarke, 2006). The question presented in this study stresses on the reason why questioning is significant for better understanding of mathematics, thus aiding in making sense and making meaning. Notably, this question poses in a timely manner, owing to the fact that mathematics entails anxiety and its impacts on teachers, as well as students is problematic, yet critical in the present technological age. Mathematics poses as a contemporary social, as well as theoretical concern and it is also relevant to the society, owing to the fact that it extends its impacts on learners, who would otherwise be regarded as children in the society. Additionally, it is evident that mathematic is relevant to the literature, owing to its potentiality to develop theory, which is presently missing from the mathematics education (Martino & Maher, 1999). This also aids in relating to the national debate that stresses on the concern why students are failing in science. The subsequent preliminary analysis of data, based on the responses of teachers and learners makes the researcher to postulate significant insights, in terms of thematic analysis in the process. Bibliotherapy poses as an iterative process, which offers teachers with the opportunity of removing obstructive feelings and reframing the manner in which they perceive themselves as learners, as well as teachers of mathematics. Furthermore, research that focuses on the explanation, as well as careful integration of certain emerging factors purpose to enable the identification of a significant relationship system between some major themes that shape the positive learning of mathematics for teachers and learners (Herbal-Eisenmann & Breyfogle, 2005). Dynamically, the related aspects comprising of the model emerges from the data and thus, allows the interaction of the vital themes, with barriers, as well as enablers that need to be identified. In this regard, the factors that hinder the process can easily be identifies and also subsequently addressed.

The extensive further data collected would make it possible for the researcher to move past the change standard analysis in in identifying the motives of learning mathematics as a response. In this regard, it will as well seek to provide the verification of the descriptive interpretation of the coding, which is completed retrospectively, whilst considering the early research projects, and as such, incorporating a detailed analysis that follows a collection of a more complex data. This can in turn be reduced in the rate of complexity, through enforcing further coding, thereby, producing a model that aids in explaining the manner in which changes occur, and the manner in which students perceive, and also negotiate tensions, based on their reflections (Nicol, 1998). The primary aim is to provide a validation and extension of the preliminary findings. Moreover, the framework used in grounded theory and content analysis in the experiences of the teachers and the learners focuses on understanding the process, based on the point of view of those who have already lived it. It is evident that this research purposes to explore on various indications, which imply on the significance that insight plays towards the development of projective motivation of the teacher and the learner towards learning mathematics, and the significant use of questions in understanding mathematics in a deeper concept. In this regard, it purposes to examine the manner in which learners perceive themselves as mathematics teachers and the manner in which this perception development in the bibliotherapy process (Vacc, 1993). This then implies that the ultimate aim in the produce a significant framework for the entire process, which aids in developing coherence and continuity, which in then flows into various mathematical units. Constant comparison, and also questioning of the data from the beginning of the research produced a theory, which is tested and also expanded by the existing subsequent studies. Notably, the scholarly literature that relates to these emerging themes guide the major concerns of the participants, who would in turn read the sources for more data. Based on the grounded research methodology, it is worth noting that the assumptions and knowledge of the researcher form a part of the data, and are compared with the data derived from the participants (Nicol, 1998). In this regard, the framework development poses as an inclusion of the consideration of the philosophy of the author, as well as the belief system. It is then vital to document the reflections of the researcher, and in order for them to be regarded as data that captures the researcher’s experiences. This poses as a significant way of ensuring that the reflections of the researcher are not separated from the entire research process. Notably, great credibility is developed, in an instance where the researcher interprets his or her own experience rather than intending to imply that the issue at hand could be detached, and as such, the researcher established an audit trail, based on his or her own personal reasoning and analysis of various issues. The effect of the research, poses as a worthwhile contribution, and as such, the experience of the researcher can be examined (Moyer & Milewicz, 2002).

Practically, it is evident that this study is very useful, owing to the fact that it provides significant insights of the strategies, which can positively inform the preparation of the teachers and the questioning strategies of the learner. Bibliotherapy is regarded as a powerful tool, in which teachers use in facilitating meta-affective changes in their preparation by encouraging them to have a reflection of their personal school experiences, as well as a reconstruction of their assessment, regarding their capacity to learn and also to understand various mathematical concepts, thus, enabling them to be able to re-examine their identity as mathematical teachers and learners as mathematical learners (Moyer & Milewicz, 2002). Ultimately, it should be noted that the idea of questioning informs the teachers, and also assists in improving the learning outcomes of the learners of mathematics. Notably, it is the teachers’ learning, which identifies their connected insights, which are negotiated, and ultimately reified. It is logical to establish the fact that teachers cannot be expect to generate the aspect of enthusiasm, as well as excitement for mathematics, in an instance where they have great fear for anxiety. Moreover, in an instance where the mathophobia is finally broken, it must be broken in entire education institution (Nicol, 1998). For these reasons, pre-service teacher education is regarded as a crucial site, which needs further research.

Conclusion

Considering the recent years, various schools have based their major focus on using research, especially digging deep into how learners learn mathematics and the implications of effective teaching practice. One of the reasons why mathematics teachers have purposed to become research informed is majorly to respond to the variety of misinformation, which are presented to the public, owing to the fact that even in an instance where a teaching practice is perceived/exposed as incorrect, it often continues to influence the manner in which teachers work. Overall, it is significant to take note of the fact that this research purposed to improve my practice in a number of ways. Firstly, it aided me in finding solutions to certain problems that arise in a classroom setting when teaching mathematics. For instance, it assisted me in determining some of the problems, which learners undergo, which hinder them from asking questions, thus leading to them having a difficulty in learning mathematics. Secondly, this research assisted me in enhancing my professional learning of significant knowledge, skills, as well as understanding. This would broaden my capabilities to be able to work effectively with mathematics learners in the future. Thirdly, it aided me to be able to connect different sources of information, as well as networks, to generally assist in supporting me professionally. Notably, different sources of information impacted me positively, to broaden my understanding. Fourthly, through this research, I was able to clarify purposes, priorities, as well as processes when introducing change. For instance, the mathematics curriculum, general pedagogy, as well as assessment. Fifthly, this research assisted me to be able to improve my understanding of my profession, as well as policy context, organizationally, nationally, and also locally, thus enabling me to be able to teach and also leader in a more strategic way, and also effectively. Finally, this research assisted me in developing my agency, influence, voice within a classroom setting, and self-efficacy within my profession. Notably, it should be noted that I did not follow the traditional approach, owing to the fact that I lack experience with it, and generally, traditional approach lacks experience with the development of researchable questions, drawing of significant conclusions, based on evidence, examination of sources critically, and even having the researcher’s mind change in an instance when he or she is confronted with data, which conflicts with a pre-conception. Additionally, it is also clear that traditional approach lacks the sense of urgency/commitment of conducting research.

Continue your journey with our comprehensive guide to Enhancing Math Learning with Manipulatives.

References

Aschner, M. J. (1961). The Language of Teaching. In O. Smith and R. Ennis, (ed.), Language and Concepts in Education. Rand McNally and Co., Skokie, Illinois.

Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative research in psychology, 3(2), 77-101.

David, O. F. (2007). Teacher’s Questioning Behaviour and. Humanity & Social Sciences Journal, 2(2), 127-131.

Herbal-Eisenmann, B. A., & Breyfogle, M. L. (2005). Questioning Our Patterns of Questioning. Mathematics Teaching in the Middle School, 10(9), 484-489.

Koo, L. C. (1999). Learning action learning. Journal of Workplace Learning, 11(3), 89-94.

Martino, A. M., & Maher, C. A. (1999). Teacher questioning to promote justification and generalization in mathematics: What research practice has taught us. The Journal of Mathematical Behavior, 18(1), 53-78.

Moyer, P. S., & Milewicz, E. (2002). Learning to question: Categories of questioning used by preservice teachers during diagnostic mathematics interviews. Journal of Mathematics Teacher Education, 5(4), 293-315.

Patel, N. V. (2003). A holistic approach to learning and teaching interaction: factors in the development of critical learners. International Journal of Educational Management, 17(6), 272-284.

Shahrill, M. (2013). Review of effective teacher questioning in mathematics classrooms. International Journal of Humanities and Social Science, 3(17), 224-231.

Vacc, N. N. (1993). Implementing the'professional standards for teaching mathematics': questioning in the mathematics classroom. Arithmetic Teacher, 41(2), 88-92.

Wragg, E. C., & Brown, G. (2001). Questioning in the secondary school. London, UK: Routledge/Falmer.