Removing Noise from Digital Images
Introduction
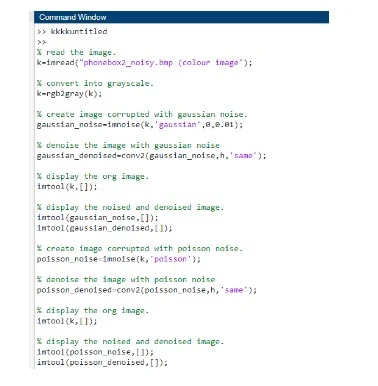
The vision systems for cameras most frequently do not use it correctly when an imaging system captures a picture hence, these images may be distorted because of the random fluctuations in intensity, variation systems or inadequate contrast, which must be addressed early in the visual processing process. The image noise of an object can be understood or defined as the random noise that does not exist in a given picture. Additionally, factors such as alteration of brightness or the colour of an image are typically a component of electrical noise. The noises from images are just an example of the unfavourable by-product of image capturing that can introduce some false and superfluous data. Hence the definition of noise was and still is the undesired signal. If you are delving into media dissertation help, exploring how all these noise factors impact image quality can be a compelling angle in place to consider. This is because unwanted electrical fluctuations in AM radio broadcasts created audible acoustic noise ("static"). Image noise can range from almost imperceptible specks on a digital photograph taken in good light to optical and radio-astronomical images that are almost all noise. A small amount of information can be extracted by sophisticated processing, but image noise is inaudible. As such, the main aim of this paper is to remove noise from digital images using the quality of latte_noisy.bmp (black & white image) and phonebox2_noisy.bmp (colour image).



Methodology
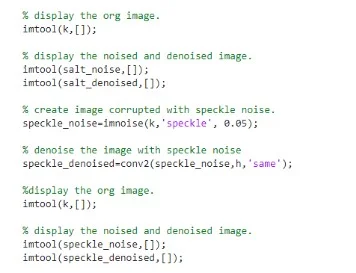
Using the data given in form of pictures from the two figures above (Figures 1 and 2), this section is going to try and reduce the noise by image filtering using the latte_noisy.bmp (black & white image) and phonebox2_noisy.bmp (colour image) to answer the questions. To understand the filters and come up with accurate results or solutions for the research, the Gaussian function model of filters will also be put into consideration in this process. This is because the Gaussian filter is a very good and most effective mechanism that can be used to remove noise from a given image. The model of Gaussian has got five properties that assist in analysing images in low pass filters for the frequency domain and the spatial frequency.
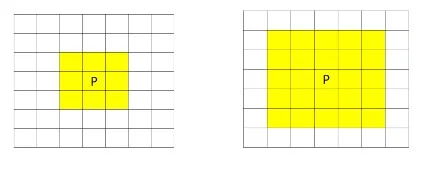
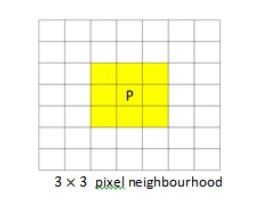
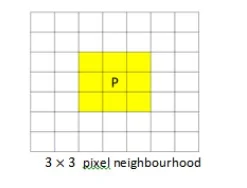
3×3 Pixel neighbourhood 5×5 pixel neighbourhood
Figure 3: Pixel neighbourhoods, highlighted yellow, for image filtering
Looking for further insights on Media Representation of Rape and Sexual Assault in the UK? Click here.
Results
The Effectiveness of Median and Mean Filters
Median filter


Median filters
Mean
mean filters
mean filters
Output
Gaussian noise output of the mean
In this process, the median value works best and could be used effectively to filter images with a lot of ease. The median filters, additionally, cannot produce very effective results if the values of one of the pixels of the neighbourhood are not given (George et al., 2018). The mean is best in this case as well, because it does not generate additional unrealistic values when it spans to the edges of the image. That is why the median filter outweighs the mean filter in terms of keeping the sharp edges of an image intact. This means that it cannot give us undesired filter output during the process. The median filter additionally examines each pixel of an image in turn and compares the image with its neighbours to determine whether or not it is typical of its surroundings. Hence, it substitutes the pixel value of the image with the median of nearby pixel values rather than the mean values. Hence, the median in the process is derived by first numerically ranking all of the pixel values that are with the image in the surrounding neighbourhood and then replacing the pixel under consideration with the middle pixel value. Nevertheless, the median utilizes the two middle values in an average way if the neighbourhood has an even number of pixels.
When a mean is taken into consideration, in this case, its average filters blur the image, hence making the image edges less apparent than in the original image. That is why it is very important to note that the mean filter has no capability of removing any particular noise effectively in the image. Hence, adopting very big and average filters may cause the picture to blur even further. As a result, the result of the image after applying the filters may be rendered worse than the original picture. Therefore, using a blurring filter to counter or diminish the details in a picture may be the ideal operation for autonomous machine recognition (Azzeh et al., 2018). They can only achieve the desired output if we are only interested in the bigger parts of the picture, such as the number of objects and the quantity of dark and bright areas. Hence, exaggerated information, in this case, may conceal the conclusion of the image. However, the filters may be used to find the best neighbourhood image by splitting the filter sizes. This may be accomplished by:
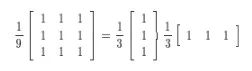
The best neighbourhood size for the filters in each case
The best neighbourhood can be archived by applying the averaging 3x3 filters to the 3x1 averaging filter to get the results that will gauge the best neighbourhood size. To obtain an effective result, this must also be archived by 1x3 averaging the filter. Nevertheless, the 3x3 average filters can be divided into two smaller filters. Hence, it can result in significant savings for the neighbours. Let's assume that n can be divided into two filters of the same sizes and hence the use of n filters necessitates multiplications and additions for each pixel that ion the picture. Because the n filter just needs multiplication and additions, the total number of addition and multiplication is this can make us believe that the ideal neighbourhood for the sizes is 3x3.
Discussion
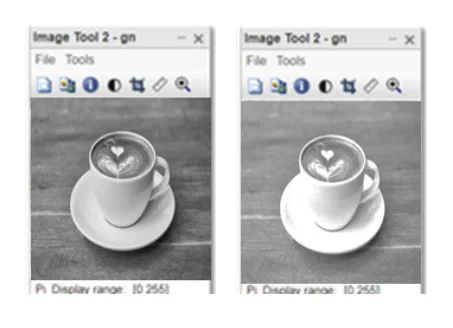
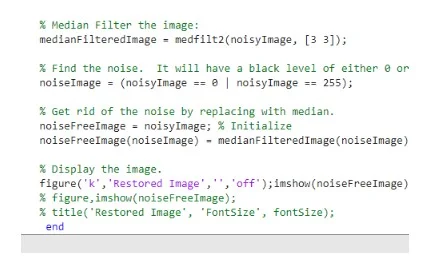
From the analysis conducted we can assume or preferably conclude that the white occurrences in the image are the ones that intensify the noise level in the picture. We managed to conclude this based on our calculations and analysis using mat lab and also relied on the Gaussian noise attribution (George et al., 2018). Gaussian states that the intensity of the images changes when it is taken from Gaussian or the normal distribution. The Gaussian noise is an excellent model for many types of sensor noise; this type of noise can be from the electronics of the camera. The averaging procedure of the local imaging has the disadvantage of blurring the strong discontinuities in the intensity of the values in a picture. To understand this, the report found that we can alternatively use a method of replacing each black or grey pixel value with that of median filters. This is because the median filters do not depend on values that are considerably different from the usual values in the area. The median values are particularly good when it comes to eliminating salt and pepper and impulsive noise in a picture while trying to maintain the feature of the picture (Fan et al., 2019). Nevertheless, the median filters, just like the linear filters, operate in successive picture windows. However, the procedure is not that important or relevant for the study, to achieve the results it is very important to consider a 3 x 3 window and compute the median of the pixels in each window center.
The report additionally found that linear smoothing can be used to remove the effects of noise in the images that were provided. The smoothing can weigh the total of the pixels in the image and uses a successive window to create a linear filter with a weight pattern that is always used in the window. In this process, the linear filter is spatially invariant and may be implemented using a convolution mask. Hence, it is spatially variable to the different filter weights when applied to the various areas within a given picture. However, the filter is still constructed as a weighted sum (Khan et al., 2019). This can lead us conclude from the analysis that a nonlinear filter is not a weighted sum of pixels. Hence, the nonlinear filters can be geographically invariant. This means that they can be able to execute the same computation given in a picture regardless of where they are in the picture or spatially changing, provided that the median filter is nonlinear and spatially invariant (Khan et al., 2019).
The results from these findings denote how you can differentiate a mean from a median and how you can build both the mean and the median filters convolution operation with equal weights in the convolution mask. Hence the degree of the filtering of an image is determined by the size of the neighbourhood ether of p 3x3 or p5x5. Hence, a bigger neighbourhood can correspond to a larger convolution mask to produce more filters that can be used to remove noise from a picture. Hence, the larger filters result in a loss of image detail as a trade-off for greater degrees of noise reduction. Additionally, it is important to note that when creating a linear smoothing filter, it is recommended that one should consider the filter weights and, hence, they should be adjusted so that the filter has a single peak, known as the main lobe, and vertical and horizontal symmetry. Linear smoothing filters are very important when it comes to noise removal because they officially eliminate the high-frequency components, resulting in a loss of visual sharpness. A step of a given change in an image will be blended into some gradual shifts, and the ability to correctly locate a change will be compromised during the process. A spatially variable filter can modify the weights to do more smoothing in a generally uniform section of the picture and less smoothing across abrupt variations in the image.


Median filter
Thanh & Surya, (2019) presents a filter that is used to modify images using the median filter known as the scalar median. This type of algorithm is quite experimental and requires an in-depth explanation to understand how it works. Hence, fooling is the formula or a notion that can be used to analyse colour images (Khan et al., 2019). in this case, we are going to consider that the colour images are represented by the alphabetical C, which is where the RGB colour is indicated, hence it states;
C=R G B or rather Cx,y= R (x,y) G(x,y) B(x,y) ,
For the equation, the C(x,y) represents the pixel vectors of an image in a given position that is indicated by (x,y) all in the colour image inC. However, the following equation indicates :
W in this equation represents the window of the odd size in the image. C(xR, yR), C(xG, yG ), and C(xB, yB) are the presentation of the coordinates of the median values in an image and represent the exact colour in the same image within the window (W) and the med R, med G, and med B represent the median operator used in the computation of the RGB colour mode or colour values. Additionally, only one component of the vector is considered at a time, so three vectors are produced. Each of these vectors has a median element as well as two assigned elements.
Conclusion
The investigation has found that the median filter is more effective than the mean filter when it comes to removing noise from an image. The maths software was used in this case to find the best or most effective filter between the mean and median filters. Additionally, the best neighbourhood size is one with the most appropriate nine sections. Finally, the report found out that the smoothing process is considered local, hence this will make the mat lab take a longer time when computing results.
Reference
Azzeh, J., Zahran, B., & Alqadi, Z. (2018). Salt and pepper noise: Effects and removal. JOIV: International Journal on Informatics Visualization, 2(4), 252-256.
Fan, L., Zhang, F., Fan, H., & Zhang, C. (2019). Brief review of image denoising techniques. Visual Computing for Industry, Biomedicine, and Art, 2(1), 1-12.
George, G., Oommen, R. M., Shelly, S., Philipose, S. S., & Varghese, A. M. (2018, March). A survey on various median filtering techniques for removal of impulse noise from digital image. In 2018 Conference on Emerging Devices and Smart Systems (ICEDSS) (pp. 235-238). IEEE.
Khan, M. Q., Hussain, A., Rehman, S. U., Khan, U., Maqsood, M., Mehmood, K., & Khan, M. A. (2019). Classification of melanoma and nevus in digital images for diagnosis of skin cancer. IEEE Access, 7, 90132-90144.
Thanh, D., & Surya, P. (2019). A review on CT and X-ray images denoising methods. Informatica, 43(2).
Khan, M. Q., Hussain, A., Rehman, S. U., Khan, U., Maqsood, M., Mehmood, K., & Khan, M. A. (2019). Classification of melanoma and nevus in digital images for diagnosis of skin cancer. IEEE Access, 7, 90132-90144.
Appendix
Median filter
median command
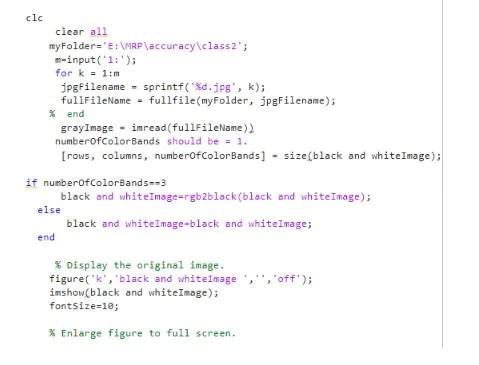
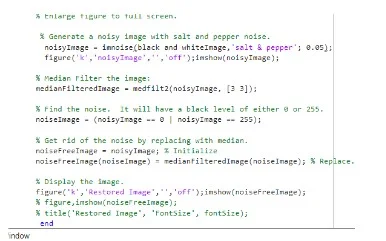
Median filters
Mean
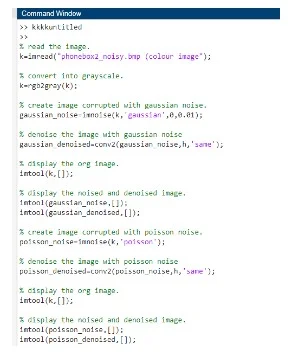
Mean filters
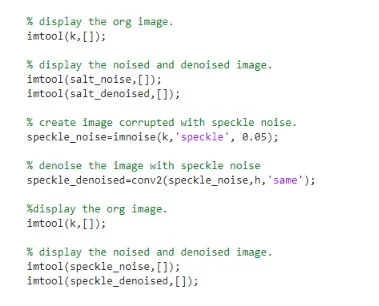
mean filters
Continue your exploration of Reflective essay on media experience with our related content.
- 24/7 Customer Support
- 100% Customer Satisfaction
- No Privacy Violation
- Quick Services
- Subject Experts



